We study an example involving the notions of probes and observers in Fiacre. The problem is to check the validity of a high-level specification pattern (see this page for information on properties in Fiacre).
We assume that you have already installed
Tina and the
Fiacre compiler, named
frac. Tina can be used to generate the state graph of a
model (files with the extension
.aut, .adr and
.ktz below). The tina distribution also provides
two model-checkers:
selt for model-checking linear (LTL) properties
and
muse for checking branching (CTL or modal
mu-calculus) properties.
The input models of Tina can be Time Petri Nets (TPN),
either in textual (.net) or graphical (.ndr)
format, or an extended notion of TPN with priorities and variables,
called a Time Transition System (TTS). TTS models can be generated by
compiling Fiacre specifications (files with the
extension .fcr below). We provide a Makefile that can be
used to compile the examples in this page. (Actually we provide two
different files, one for UNIX-like OS and the other for Windows.) You
must edit the Makefile to specify the path to your local installation of
Fiacre (variable
FRACLIB) and the type of operating system (variable
HOSTTYPE).
Simple Example of Observers and Properties in Fiacre: the Computer Mouse Example
Our first model is a simple version of the specification of a computer
mouse with a double click in Fiacre. We provide two versions of the
model: first a Fiacre model with two property declarations
(file mouseProperty.fcr); then the same model with a
different property expressed using an observer
(file mouseObserver.fcr). This is the example used for
describing the Fiacre language in the companion paper
[TTCS15].
Files with the extension
.fcr can be compiled into a TTS using
the frac compiler. Using the Makefile provided
with the source files we can generate the TTS files using the
following command. (We use the symbol
$> for the shell prompt.)
$> make mouseObserver.tts
frac -obs .\mouseObserver.fcr .\mouseObserver.tts
gcc -m32 -DMINGW -O2 -o
.\mouseObserver.tts\mouseObserver.dll -shared -I
C:\Users\...\frac-2.2.4\lib -I C:\Users\...\frac-2.2.4\lib\avl
.\mouseObserver.tts\mouseObserver.c
We can generate the state space of the TTS model using
the tina tool. The following command will generate
a state graph in compressed form (extension .ktz);
it is possible to list the data in this file using
the ktzio tool.
$> tina .\mouseProperty.tts mousep.ktz
# net process_____presentAfter____2__1_________presentAfter________1____1__Computer____1____User____1____Push____1, 19 places, 19 transitions# # bounded, not live, possibly reversible # # abstraction count props psets dead live # # states 1836 19 ? 0 40 # # transitions 2407 19 ? 1 11 #
$> ktzio .\mousep.ktz
Checking the Properties in File mouseProperty.fcr
The model in mouseProperty.fcr has two property
declarations:
property foo is present (Main/3/state two) after (Main/2/state quick) within [1,2] property bar is present (Main/3/state two) after (Main/2/state slow) within [0,100]
These properties are related to events declared in the main component
of the specification (called Main), see the code excerpt
below. Hence, for example, the declaration Main/2 targets
the events of the second process instance in the parallel composition
in Main (that is an instance of the
process User)
component Main is port click, single, double : none in [0,0] par * in Mouse [click, single, double] || User [click] || Computer [single, double] end Main
The computer mouse model is composed with two other processes, modeling
a User and a Computer, which describes the behavior of the
environment. Property foo states that after the User presses
quickly in the mouse button (it is in state quick) then we
must observe the process Computer in state two
between 1 and 2 units of time.
Properties are automatically translated into LTL formulas (see the
file mouseProperty.tts/mouseProperty.ltl in the generated
TTS) that can be checked as follows. We use the command line
options -b -q to simply print the truth value of the two
asserts directives. You can find more information on
the manual
pages of selt
$> selt -b -q .\mousep.ktz .\mouseProperty.tts\mouseProperty.ltl
TRUE FALSE
Checking the Properties in File mouseObserver.fcr
The model in mouseObserver.fcr has a single property. This
is a LTL formula stating that the observer NeverTwice will
never reach the state error. The command-line
option -obs of frac is necessary when
compiling a model that uses observers.
property safe is ltl [] not (Obs/1/state error)
In this model, the Obs is
not part of the main component but it can observe
when Computer enters its state named two using
the probe p (the probe is declared as enter
(Main/3/state two)). Hence the property safe is true
only if Computer cannot enter twice in the
state two. This can be checked using the following
command.
$> tina mouseObserver.tts mouseo.ktz
...
$> selt -q .\mouseo.ktz .\mouseObserver.tts\mouseObserver.ltl
FALSE state 0: Computer_1_sstart NeverTwiceA_1_sidle Push_1_ss0 User_1_ss0 -User_1_t1_Push_1_t0 ... (preserving T)-> state 32: Computer_1_sstart NeverTwiceA_1_serror Push_1_ss0 User_1_sslow -User_1_t2 ... (preserving NeverTwiceA_1_serror)-> state 33: Computer_1_sstart NeverTwiceA_1_serror Push_1_ss0 User_1_ss0 [accepting all]
The property is false and selt outputs a summary of the
counter-example that was found. It is possible to print a
counter-example in full, using option -p, or to save it
into a scenario file.
Generating the State Class Graph for a Property Pattern
In the second part of this tutorial, we generate a state class graph
corresponding to the possible behavior of an observer for the pattern
"present
a after b within
[4, 5[". The graph is obtained by composing an observer for the
pattern (the process Present) with a process that can
generate arbitrary timed traces (called Universal in our
article [TTCS15]). This corresponds to the Fiacre
model universalpresent.fcr that is part of our source
files
We can generate a textual version of the state graph (file
extension .aut) using the following command. We use
option -F1 of tina to generate a state space
with a discrete time semantics. You can also generate the
file univ.aut using the Makefile (with the
command make present)
$> frac -obs universalpresent.fcr universalpresent.tts
$> tina -F1 universalpresent.tts univ.aut
WARNING: dense traces not preserved, some priorities # net process_Present__1_Universal__1, 6 places, 7 transitions # # bounded, not live, not reversible # # abstraction count props psets dead live # # states 26 0 ? 0 6 # # transitions 43 7 ? 0 3 #
The labels of the state graph in univ.aut are generated
from the names of the processes together with an identifier,
e.g. t0, that identifies uniquely a transition in the
process. The AUT format (also
called Aldebaran
format) is a simple textual format for representing labelled transition
systems that can be used with several model-checking toolboxes. An AUT
file can be opened in the nd tool; this is an editor and
TPN simulator that is part of the Tina distribution (see for
example here).
It is possible to generate a graphical version of the graph using an
automatic layout; just go to the menu toolbar in nd,
under Edit > draw then choose a layout algorithm.
In the remainder of this work, we use a version of the AUT file where
labels are renamed to follow the convention in our paper. This is the
file verif.aut below. We also provide a graphical version
of the file.
- verif.aut
- verif.adr (same system, graphical file)
- verif.ktz (same system,
compressed format, can be obtained with the command
ktzio .\verif.aut .\verif.ktz)
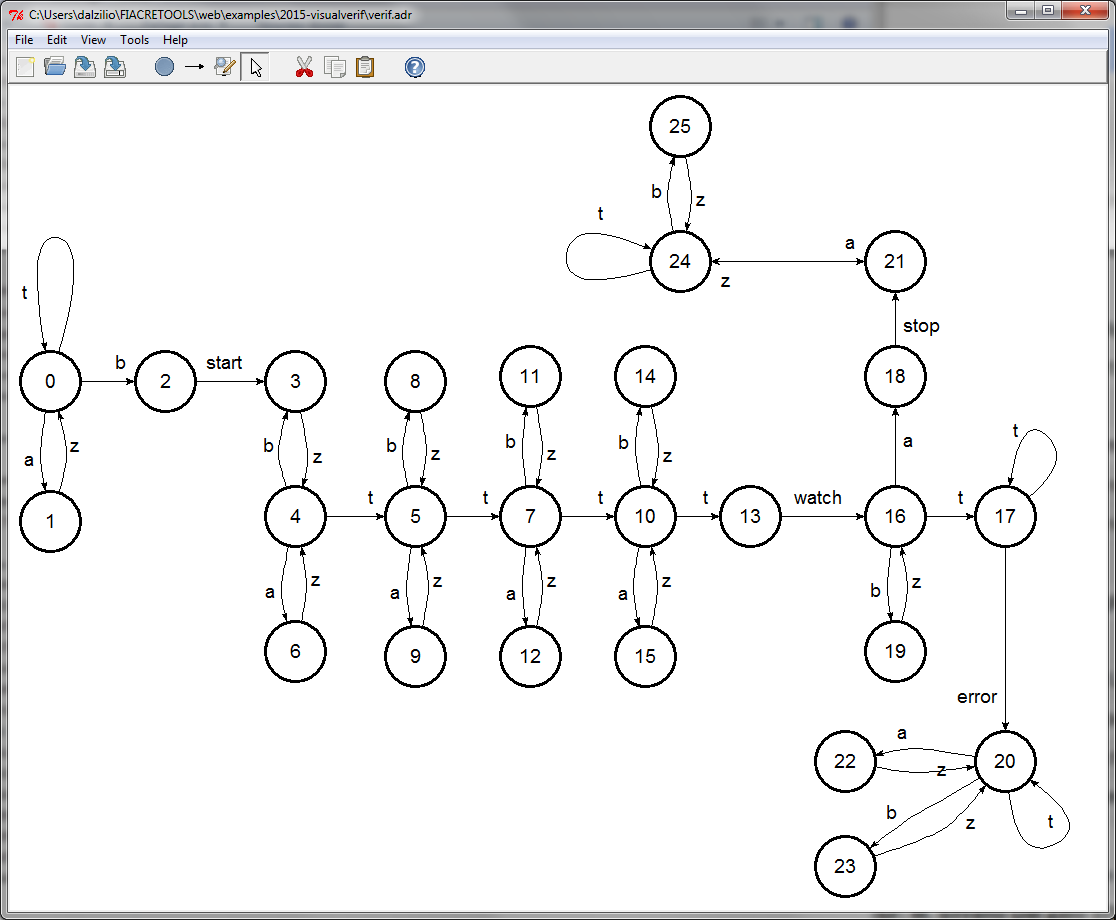
The next step is to study the soundness and the completeness of our
observer with respect to the semantics of the pattern. We remark in the
paper [TTCS15 that, in the discrete time case, it is possible
to define the semantics of the pattern using a regular (path)
expression. Namely, if Tick stands for the expression t
. (-t)* then we have:
Pres = (-b)* \/ ((-b)* · b · (- t)* · Tick · Tick · Tick · Tick · a · T*)
Checking the Soundness of the Observer using LTL
It is a folklore result that regular expressions can be interpreted as temporal logic formulas. Next, we use the connection between regular expressions and LTL to check the soundness of the Present observer. We study the limitation of this approach and show that the use of a branching logic is more interesting.
We can use LTL formulas to interpret regular expressions. For instance
the expression (-b)* (never b) can be
interpreted by the formula [] -b (always
not b). More generally, the (finite) traces matching the
expression Pres can be encoded with the following formulas
and checked using selt.
$> more .\present.ltl infix L o R = L /\ ()R; infix L * R = L U R; op TICK R = t o ((- t) * R); op Phi1 = [] - b; op Phi2 = (-b) * (b o ((-t) * (TICK (TICK (TICK (TICK (a o T))))))); (Phi1 \/ Phi2) => ([] - error); ([] - error) => (Phi1 \/ Phi2); $> selt -b -q .\verif.ktz .\present.ltl TRUE FALSE
Soundness means that, for every trace matching Pres, the
observer should not reach state error. This is the first
implication in our script. The reverse property is false. Actually this
is a limitation of the approach, that is based on a linear time
logic. The problem lies in the treatment of time divergence (and of
fairness)./p>
Checking the Soundness of the Observer using Model mu-Calculus
Like in the previous section, we show how to interpret regular expressions over traces using a temporal logic. In this case, the target logic is a µ-calculus with modalities for forward and backward traversal of a graph. The following script is the one described in our paper.
$> muse -b -q .\verif.ktz .\present.mmc ... EQUIV : states TRUE
Files Available on this Use Case
Everything in a single archive file.
Fiacre files and Makefiles
- Makefile (UNIX version)
- Makefile (Windows version)
- mouseProperty.fcr
- mouseObserver.fcr
State Graph Files for (Universal || Present)
Scripts for selt and muse
References
[TTCS15] Automating the Verification of Realtime
Observers using Probes and the Modal mu-calculus. Silvano Dal Zilio
and Bernard Berthomieu,

