Diagnosability of Patterns and Single-Faults

Silvano
Apr 5, 2020

This post is part I of a series of articles describing how to reproduce the experiments reported in our 2020 (submitted) paper about Twina. We assume that you already installed Twina and a recent release of Tina. You can also install a Docker image containing all the necessary tools, scripts and model files:

docker pull vertics/twina

Diagnosability of Single-Faults

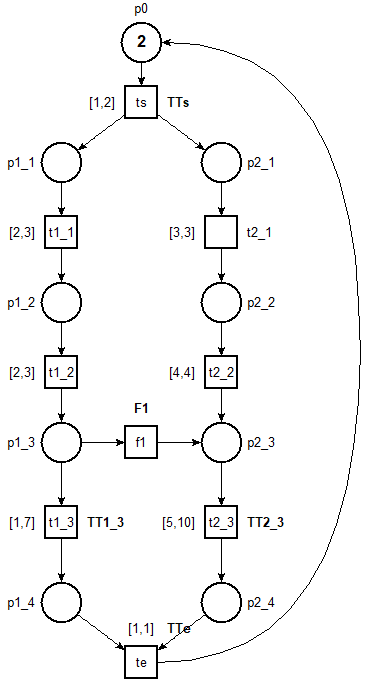
We have three different methods for deciding the diagnosability of a single fault. Each method use a different option provided by Twina. We give, in each case, an example of how to apply these methods taking as model a simple instance of the WODES diagnosis benchmark of Giua with added timing constraints ( wodes ) and the fault label $F1$. This system is not diagnosable.

The TPN wodes.ndr (drawn from wodes.net using nd)
  1. the first method relies on option -twin, that computes the state class graph for the “twin-product” of a net given a fault label $f$. In this case we need to check the LTL formula (<> f) => (<> dead);
  2. the second method relies on the use of the PTPN scripting language to build the twin plant model. We give more explanation on this construction below. In this case we need to check the LTL formula (<> f.1) => <>(f.2 \/ dead);
  3. the last method relies on option -diag, for testing diagnosability of single faults using a dedicated on-the-fly algorithm (meaning that we avoid computing the whole state space of the system when not necessary). When the system is not diagnosable, it is possible to print a counter-example using the verbose output mode, option -v

For method (1) and (2), we need to compute the state class graph in a format than can be used as an input with selt, our LTL model-checker. (We only need information regarding the labels of transitions.) To this end we use a combination of options -aut and -lt and the ktzio tool from the Tina toolbox. Options -q and -b of selt are used to print only the truth value of the formula.

Method 1

$ twina -twin --fault=F1 -lt -aut wodes.net | ktzio -AUT - wodes.ktz
$ selt -q -b wodes.ktz -f "(<> F1) => (<> dead);"
FALSE

We generate a SCG with 55 402 classes, corresponding to a ktz file of size 284K. The overall computation time is about 3s.

Method 2

$ cat wodes.tpn
load wodes.net
ren F1.1/F1
load wodes.net
ren F1.2/F1
intersect TTe TTs TT1_3 TT2_3
$ twina -aut -lt wodes.tpn | ktzio -AUT - wodes.ktz
$ selt -q -b wodes.ktz -f "(<> {F1.1}) => <>({F1.2} \/ dead);"
FALSE

We generate a SCG with 205 140 classes, corresponding to a ktz file of size 1.2M. The overall computation time is about 12s. We can further simplify this method by removing the transitions with label F1.2 in the result (and use the same approach than in method 1).

Method 3

$ twina -diag --fault=F1 -twin wodes.net

# net is not diagnosable
# length:              54
#
# states (explored):   293
# markings:            97
# dbms:                289
0.003s

This method is generally better when the system is not diagnosable. In our example, it returns a result after exploring only 293 classes (instead of 55 402). We also do not need to serialize the SCG before loading it in the model-checker. On the opposite, this approach enumerates the Strongly Connected Components of the system. Hence it may be less beneficial when the system is diagnosable.

Pattern Diagnosability

Our method can be naturally extended to check for the diagnosability of patterns of unobservable events. In our case, a pattern $M$ is a special instance of TPN. We denote $F$ the set of labels occurring in $M$ and we distinguish a place in $M$, say found, that is a witness for detection.

Instead of defining a pattern as a regular language, or as a set of timed sequences, we use instead the timed language of $M$. Hence we restrict ourselves to time regular languages, meaning sets of executions that can be realized with a TPN. This is enough to model every regular set of (untimed) traces.

The TPN/pattern omega.ndr for “at least three F1 before a F2” (drawn from omega.net using nd)

We also want to make sure that a pattern does not interfere with the system it interacts with. For example, it should not prevent some executions of the system. To this end, we impose three well-formedness conditions on patterns:

  1. patterns are total; they should always allow transitions on the labels in $F$, at any time (they never block or delay a transition)
  2. patterns are deterministic (the same observations should lead to the same states)
  3. labels in $F$ are unobservable

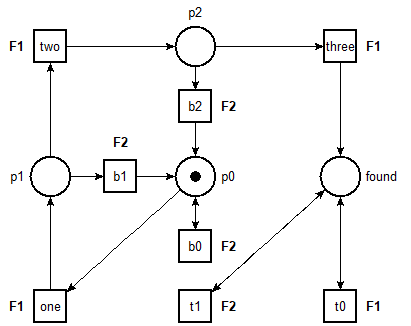
We use an example based on the model of a product transportation system with added timing constraints ( transport_timed ) and the pattern ( omega ) display in Fig. 2.

By analogy with our previous definition of diagnosability, we say that pattern $M$ is diagnosable if it is not possible to find a (critical) pair of executions such that $M$ is found in one but never in the other. We can again reduce this question to a model-checking problem on a twin-plant; this time on the product of the system with the pattern.

$ cat transport.tpn
load transport_timed.net
load omega.net
intersect
dup 1
intersect U D PR1 PR2 ERR1 ERR2 ELR1 ELR2
$ twina -kaut transport.tpn | ktzio -tina -AUT - transport.ktz
$ selt -q -b transport.ktz -f "(<> {found.1.1}) => <>({found.1.2} \/ dead);"
TRUE

Unlike the previous methods, we need to generate a SCG that contains information about the markings of each state; hence the use of option -kaut with Twina. We also need to adapt the LTL formula to check whether we found the pattern in the first or second component of the product.

The pattern is diagnosable in the (timed) instance of the transport model that we use ( transport_timed ). At the opposite, the pattern is not diagnosable if we use the untimed version ( transport.net ).

Examples used in this post

patterns