Reproducing the Benchmarks of our 2020 Paper

This post is part II of a series of articles describing how to reproduce the experiments reported in our 2020 (submitted) paper about Twina. See part I.

Pattern Diagnosability on the Product Transportation System

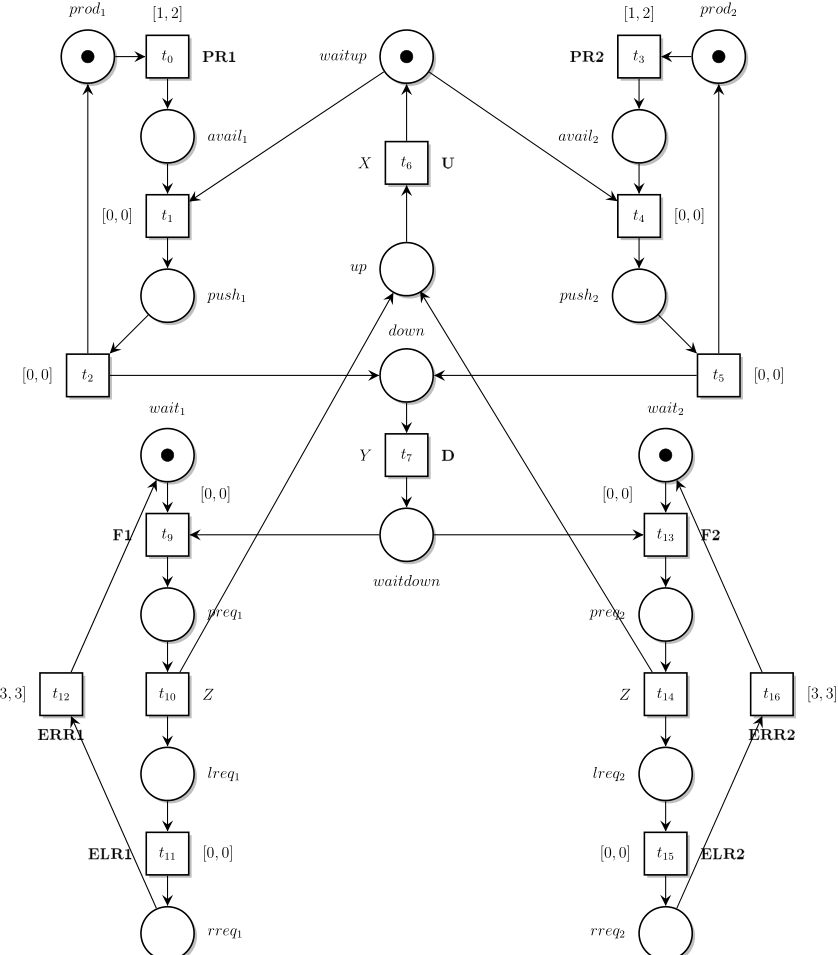
In this post we consider the model of a product transportation system with added timing constraints displayed in Fig. 1.

As in part I, we consider the diagnosability with respect to omega , a pattern for property “at least three F1 before a F2”. Hence the observable labels in this example are U, D, PR1, PR2, ERR1, ERR2, ELR1 and ELR2.

It is possible to check the diagnosability of the pattern using a sequence of bash commands such as:

$ cat transport.tpn
load transport_timed.net
load omega.net
intersect
dup 1
intersect U D PR1 PR2 ERR1 ERR2 ELR1 ELR2
$ twina -kaut transport.tpn | ktzio -tina -AUT - transport.ktz
$ selt -q -b transport.ktz -f "(<> {found.1.1}) => <>({found.1.2} \/ dead);"
FALSE

We have tested the diagnosability of the system for several choices of timing constraints for the transitions t6 (label U, denoting a product going Up the elevator), t7 (label D, denoting a product going Down the elevator), t10 and t14 (silent, non-observable transitions.). The result depends on the timing constraints: let X be the (static) time interval for t6, Y for t7 and Z for t10 and t14.

• $X = Y = Z = [0, \infty[$: the system is not diagnosable and has 126 548 classes. The system without any timing constraint leads to a state space with 14 270 markings
• $X = Y = [0, \infty[$ and $Z = [0, 6]$: the system is not diagnosable and has 129 096 classes
• $X = Y = [0, \infty[$ and $Z = [1, 6]$: the system is diagnosable and has 15 848 classes
• $X = Y = [1, 10]$ and $Z = [0, \infty[$: the system is diagnosable and has only 2186 classes

The time needed to generate the state space in the most complex case is about 4.5s on a laptop (see model transport_bigger ), and under 10ms for the models with less than 20 000 classes.