Inhibition and Permission TPN (IPTPN)

Berthomieu et al. [PBV2011] define an extension of TPN with inhibition and permission that provides a method for building composable nets; meaning TPN where all observable transitions have trivial time constraints (their time interval is $[0, \infty[$]). With this extension, it is always possible to build a composable IPTPN from a TPN.

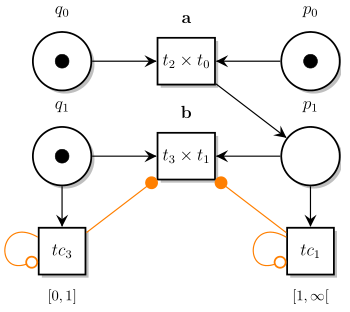
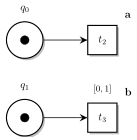
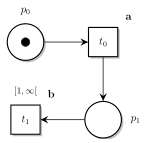
For example, Fig. 1 and 2 below display two TPN and Fig. 3 displays the IPTPN corresponding to their product. In this construction, we create a silent, extra-transition $tc_i$ for every non-trivial observable transition $t_i$. These transitions cannot fire (they self-inhibit themselves with an inhibitor arc —○) but “record the timing constraints” of the transition they are associated with. Then a permission arc ( —●) is used to transfer these constraints on the (product of) labeled transitions.

Option -iptpn is used to generate a TPN (in .net or .tpn syntax) that can be analyzed using Tina. This option can be used to generate an IPTPN from: (1) the product of two nets (together with option -I); (2) the “twin-plant” construction (-twin); or (3) just from a single net alone. In the resulting net, the silent (timed) transition corresponding to $tc_i$ is named {ti.t}.

$ twina -iptpn -fault=a C1.net
#
# net C1
# 2 places, 2 transitions + 1 tc transitions
#
pl p0 (1)
pl p1 (1)
tr t0 : a [0,w[ p0 ->
tr t1 : b  p1 ->
tr {t1.t} [0,1] p1 ->
pr {t1.t} -o {t1.t}
pr {t1.t} -* t1

To use the resulting net with Tina you only need to set an environment variable called IPTPN (to a non-zero value). Then you may directly pipe the result to Tina, like in the following example. (our example below use sift, an optimized tool for state-space generation.)

$ export IPTPN=1
$ twina -iptpn -I C1.net C2.net | sift -
3 marking(s), 3 domain(s), 3 classe(s), 2 transition(s)
0.000s

Examples used in this post

The basic examples of nets used in our paper C1.net and C2.net .