Contents
General information
R-RoMulOC is coded using objects in Matlab format. These objects and related functions are described below. For a display in Matlab of all available functions:
>> help romuloc
For demos of what R-RoMulOC does:
>> romuloc
You will be guided to one of the four demo examples.
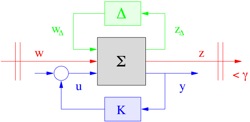
Robust analysis of an LFT-type uncertain system
Based on some equations of a mechanical system, LFT modelling is illustrated including several types of uncertainties. Pole location and H-infinity performance are analysed with both probabilistic and deterministic methods (inclding parameter-dependent Lyapunov type tests).
Robust analysis of a polytopic-type uncertain system
The example is an academic example with robust H2 performance analysis. Conservatism of parameter-dependent Lyapunov function results is shown to be less than that of "quadratic stability" results. It is even proved to vanish in the present case. A worst case value of the uncertainties is extracted from the solution of the dual SDP problem.
Multi-objective robust state feedback design for an LFT-type uncertain system
The model is that of one axis motion of 3DOF-helicopter benchmark from Quanser. State-feedback is requested to guarantee for all uncertainties two pole location constraints plus an H-infinity performance level.
Multi-objective robust state feedback design for a polytopic-type uncertain system
The model is that of one axis motion of 3DOF-helicopter benchmark from Quanser. State-feedback is requested to guarantee for all uncertainties a pole location constraint plus an H-infinity performance level. Both deterministic and randomized methods are tested.

Objects
R-RoMulOC code involves six objects used to encapsulate data in compact format with nice display. Manipulations of these objects allow the user to build and solve control problems. The six classes of objects are given below.
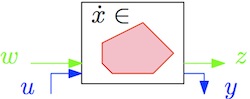
State-space models with 3 types of inputs and outputs
Systems in R-RoMulOC are defined in state-space. They can be continuous-time or discrete-time. The main difference with
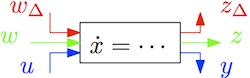
One pair of inputs/outputs is the classical control input (u) / measured output (y) pair. Default, when computing a feedback with some controller, these are the signals that are used to close the loop. The second pair of inputs/outputs (w/z) are intended for performance definition (guarantee for example an upper bound on the norm of the performance output z for norm bounded perturbations w). Finally, a pair (wd/zd) is used to define exogeneous feedback with uncertainties (used for LFT models). Notations for matrices of an
dx = A*x + Bd*wd + Bw*w + Bu*u
zd = Cd*x + Ddd*wd + Ddw*w + Ddu*u
z = Cz*x + Dzd*wd + Dzw*w + Dzu*u
y = Cy*x + Dyd*wd + Dyw*w + Dyu*u
Note that RoMulOC also allows the definition of arrays of systems, that is, a finite collection of models that share same dimensions of state, input and output vectors.
A typical and most simple way to declare a system in R-RoMulOC format is as follows:
>> sys = ssmodel('My plant');
>> sys.Bu = [1 0; 0 0.1 ; 0 0 ];
>> sys.A = [-1 0 0; 0.1 -2 0.2; 0.1 0.1 -1];
>> sys.Cy = [0 0 1];
>> sys.Bw = [1 ; 0 ; 0];
>> sys.Cz = [0 1 0];
>> sys
name: My plant
n=3 mw=1 mu=2
n=3 dx = A*x + Bw*w + Bu*u
pz=1 z = Cz*x
py=1 y = Cy*x
continuous time ( dx : derivative operator )
>> sys.A
ans =
-1.0000 0 0
0.1000 -2.0000 0.2000
0.1000 0.1000 -1.0000
Block diagonal uncertain operators
On of the two types of uncertain models considered R-RoMulOC is LFT modelling where the uncertainties enters the plant as a feedback loop. There can be multiple uncertainties all entering as a loop, thus defining a block diagonal uncertainty operator.
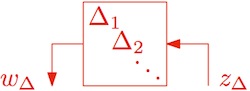
There are many types of uncertainties in R-RoMulOC providing many flexibilities. There is for example no need to a priori normalize these in set centered at zero and norm bounded by one. Moreover, the data you enter is kept the way you defined it, except if you decide to modify it. Below is an example involving two types of uncertainties. One is interval uncertainty which is a subcase of polytopes. The other is the classical norm-bounded uncertainty. Both can be combined in a block diagonal operator where blocks can be repeated and need not to be ordered.
>> di = uinter( [-1 1; 0 1] , [1 -1; 0 -1] )
wd = #1 * zd
index size repeat. RorC dist. nature
#1 2x2 1 real det. LTI interval 3 param
>> dp = upoly( d1 )
wd = #2 * zd
index size repeat. RorC dist. nature
#2 2x2 1 real det. LTI polytope 8 vertices
>> dn = unb( 1, 2, 1.2 )
wd = #3 * zd
index size repeat. RorC dist. nature
#3 1x2 1 real det. LTI norm-bounded by 1.2
>> D = diag( di, dn, di )
diagonal structured uncertainty
size: 5x6 | nb blocks: 3 | independent blocks: 2
wd = diag( #1 #3 #1 ) * zd
index size repeat. RorC dist. nature
#1 2x2 2 real det. LTI interval 3 param
#3 1x2 1 real det. LTI norm-bounded by 1.2 LTI systems with uncertainties
There are two types of uncertain models in R-RoMulOC, namely LFT models and polytopic models. Both are contained in the
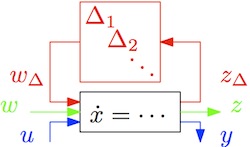
An example of LFT-type uncertain system definition is given below:
>> sys = ssmodel;
>> sys.A = -eye(3);
>> sys.Bd = eye(3);
>> sys.Cd = ones(3,3);
>> sys.Ddd = 0.1*ones(3,3);
>> d1 = unb(2,2,1.2);
>> d2 = uinter(-1,1);
>> D = diag(d1,d2);
>> usys = ussmodel( sys, D)
Uncertain model : LFT
-------- WITH --------
n=3 md=3
n=3 dx = A*x + Bd*wd
pd=3 zd = Cd*x + Ddd*wd
continuous time ( dx : derivative operator )
-------- AND --------
diagonal structured uncertainty
size: 3x3 | nb blocks: 2 | independent blocks: 2
wd = diag( #1 #2 ) * zd
index size repeat. RorC dist. nature
#1 2x2 1 real det. LTI norm-bounded by 1.2
#2 1x1 1 real det. LTI interval 1 param
The second type of uncertain systems is the class of polytopic systems, which include as special cases the parallelotopes and the intervals.
An example of such models is given below:
>> sys1 = ssmodel;
>> sys1.A = [-1 1;0 -1];
>> sys2 = ssmodel;
>> sys2.A = [1 -1;0 1];
>> usysi = uinter( sys1, sys2)
Uncertain model : interval 3 param
-------- WITH --------
n=2
n=2 dx = A*x
continuous time ( dx : derivative operator )
>> usysp = upoly(usysi)
Uncertain model : polytope 8 vertices
-------- WITH --------
n=2
n=2 dx = A*x
continuous time ( dx : derivative operator )
>> usysp(4).A
ans =
1 -1
0 -1
Analysis and control design problems
Once some plant (or several) plants have been defined in R-RoMulOC, building LMIs for some control problem to be solved is a matter of one line of code. In the example below we assume some uncertain plant has been defined (it is the one coded in the
>> usinf
Uncertain model : LFT
-------- WITH --------
name: shaped model
n=8 md=6 mw=2
n=8 dx = A*x + Bd*wd + Bw*w
pd=7 zd = Cd*x + Ddd*wd + Ddw*w
pz=1 z = Cz*x + Dzd*wd
continuous time ( dx : derivative operator )
-------- AND --------
diagonal structured uncertainty
size: 6x7 | nb blocks: 4 | independent blocks: 4
wd = diag( #3 #4 #5 #6 ) * zd
index size repeat. RorC dist. nature name
#3 1x2 1 real det. LTI {X,Y,Z}-dissipative Inertia
#4 2x2 1 real det. LTI norm-bounded by 0.25 Damping
#5 1x1 1 real det. LTI interval 1 param Input
#6 2x2 1 real det. LTI polytope 3 vertices Output
>> Hi_1 = norm( usinf, Inf )
Nominal
Hi_1 =
1.6027
>> pb2 = ctrpb('analysis','rand') + hinfty( usinf );
>> Hi_2 = solvesdp( pb2 )
459 tested random values out of 459 | worst case performance = 2.480e+00
Hinfty norm = 2.48034 is the worst case estimate
The probability P for an other sample to violate the estimate is such that
Prob{ P > 0.01 } less than 0.01
Hi_2 =
2.4803
>> pb3 = ctrpb('analysis') + hinfty( usinf )
control problem: ANALYSIS
Lyapunov function: UNIQUE (quadratic stability)
Specified performances / systems:
# minimize HINFTY / shaped model
>> Hi_3 = solvesdp( pb3 )
[...computation...]
Hinfty norm less than 2.86659 assessed
Hi_3 =
2.8666
pb4 = ctrpb('analysis','PDLF') + hinfty( usinf )
control problem: ANALYSIS
Lyapunov function: QUADRATIC-LFT
Specified performances / systems:
# minimize HINFTY / shaped model
>> Hi_4 = solvesdp( pb4 )
[...computation...]
Hinfty norm less than 2.52258 assessed
Hi_4 =
2.5226
Regions for robust pole location
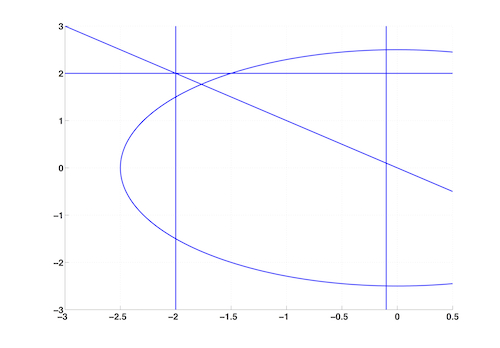
In RoMulOC stability and pole location specifications are internally coded in a unified manner. Stability of continuous-time systems is the pole location in the left half of the complex plane. Stability of discrete-time systems is the pole location in the unit disc centered at the origin. Other pole location regions that may be defined are half planes that pass by any point of the complex plane and with any inclination with respect to the imaginary axis and discs centered at any point of the complex plane and with any radius.
Some examples or regions are as follows (with their interpretation on the modes of continuous time systems):
- a half plane such that the real part of the poles is less than -0.1 (guarantees time constant to be less than 10s).
>> r1 = region('plane',-0.1,0);
- a half plane such that the real part of the poles is greater than -2 (guarantees time constant to be greater than 0.5s).
>> r2 = region('plane',-2,pi);
- a half plane crossing the origin with angle of 45deg with respect to the imaginary axis (guarantees damping to be greater than sin(pi/4)=0.7071).
>> r3 = region('plane',0,pi/4);
- a half plane crossing 2j with angle of 90deg with respect to the imaginary axis (guarantees damped natural frequency to be less than 2rad/s).
>> r4 = region('plane',2j,pi/2);
- a disc centered the origin with radius 2.5 (guarantees natural frequency to be less than 2.5rad/s).
>> r5 = region('disc',0,2.5);
The regions can be plotted as follows.
>> axis([-3 0.5 -3 3]), grid, hold on
>> plot(r1), plot(r2), plot(r3), plot(r4), plot(r5)
Matrix ellipsoids - generaliation of norm-bounded constraints
Robustness is in the litterature most often with respect to uncertain operators defined as norm bounded, that is, in the case of linear applications (matrices), uncertainties centered at zero and with bounded L2-induced norm by usually 1. A generalization of such sets of matrices is the case of sets defined by a quadratic matrix inequality. Some examples follow.
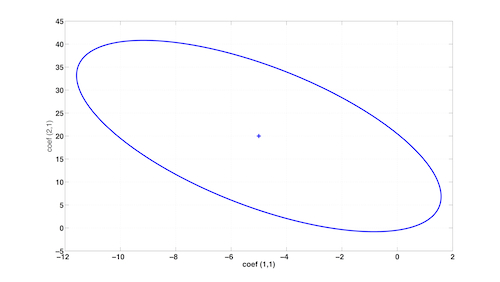
Ellipsoids of 2-by-1 matrices, that is of vectors of R^2.
>> e1=melli(-1,[1 -1],[1 0.2;0.2 0.1])
{X,Y,Z}-ellipsoid of real valued 2 x 1 matrices
>> center(e1)
ans =
-5.0000
20.0000
>> plot(e1);
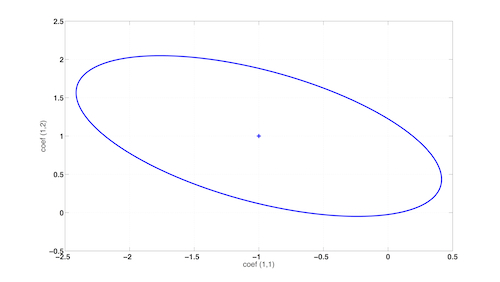
Ellipsoids of 1-by-2 matrices, which can by bijections be represented as vectors in R^2.
>> e2=melli([-1 -0.2;-0.2 -0.1],[1;-1],1)
{X,Y,Z}-ellipsoid of real valued 1 x 2 matrices
>> center(e2)
ans =
-1 1
>> plot(e2);
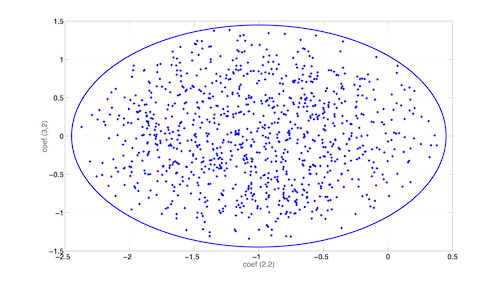
Ellipsoids of 3-by-2 matrices, for which one can plot projections on pairs of coefficients. It is also illustrated here that uniform sampling over such sets is made possible (uses sampling tools from RACT).
>> e3=melli([-1 -0.2;-0.2 -0.1],[1 0 1;-1 1 0],eye(3))
{X,Y,Z}-ellipsoid of real valued 3 x 2 matrices
>> center(e3)
ans =
-1 1
0 -1
-1 0
>> plot(e3,2:3,2);
>> hold on
>> e3samples=usample(e3,1000);
>> plot(reshape(e3samples(2,2,:),1,[]),reshape(e3samples(3,2,:),1,[]),'+','LineWidth',3)

projects.laas.fr/OLOCEP/rromuloc - last update 6-Jun-2014