Papers
References for results coded in R-RoMulOC
R-Romuloc aims at gathering many results and combinations of theses. The number of cases and subcases is large. Thus some of the coded formulas may be unpublished. Below we indicate the key references applied in the toolbox.
LMI results for LTI systems without uncertainties
Given an LTI system without uncertainties, the user has access to the LMIs for stability, H-infinity, H-2 or impulse-to-peak perormances. These LMIs are nowadays classical and can be found in [Boy94]. In addition to these performances, the user has access to pole-location (D-stability) LMI tests. These LMIs correspond to the ones proposed in [Pea00scl].
Robust LMI tests for polytpic uncertain systems
One of the two classes of LTI systems with uncertainties considered in R-RoMulOC is the class of polytopic systems described as the linear convex combinations of a finite number of vertices. For these, results that are coded include the ``quadratic stability" results based on [Bar85] (use of a unique Lyapunov matrix for all uncertainties). In addition to these results, the toolbox includes less conservative results involving slack variables and polytopic parameter-dependent Lyapunov matrices. The LMIs of these results are based on the technique described for pole location performance in [Pea00]. The exact formulas of the LMIs for the other performance criteria can be found in [PeaPhd]. It is worth mentionnning that on particular examples the LMIs that are actually solved may be of smaller dimensions than the ones in [PeaPhd]. The size reduction of LMIs follows the results from [Pea09] and improved in [Pea14a]. When solving any of the LMI conditions for robust analysis of polytopic systems, the user can ask for a worst case estimate (a realisation of the uncertain plant that is expected to be close to violating analyzed performances). The computation of that worst case estimate is based on results in [Sch05], or more precisely as reformulated in [Ebi11].
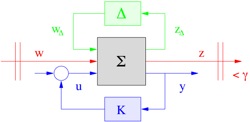
Robust LMI tests for LFT uncertain systems
The second class of uncertain systems considered in R-RoMulOC is those modeled via Linear Fractionnal Tranfromation (LFT), that is, composed of an LTI system in feedback loop with an uncertain operator. The uncertain operator is assumed block-diagonal where identical blocks can be repeated, each of which being either dissipative (which includes norm-bounded and passive blocks as special cases) or polytopic. LMI results are derived following the quadratic separation methodology [Iwa98] with separators borrowed from mu-analysis, IQC-framework, full-block S-procedure, as well vertex separators. The generalization of the separator construction to all considered uncertainties follows lines exposed in [PeaPhd]. The methodology exposed in [Iwa05] for dealing with frequency ranges is also included. For the class of LFT uncertain models there are two types of results that are coded. One is based on unique for all uncertainties Lyapunov matrices. The seconds involves parameter-dependent Lyapunov matrices with quadratic-LFT dependency with respect to uncertainties. These results are inspidered by [Iwa01]. There are a simplified version of the results in [Pea01]. They correspond to the first step in the relaxations described in [Pea07].
LMIs for multi-objective state feedback design
The current version of R-RoMulOC contains state-feedback multi-objective design features. These include the classical Lyapunov Shaping paradigm approach (one Lyapunov matric for all uncertainties and all perfromance specifications) [Sch97] and linearized using the chage of variables proposed in [Ber89]. In addition to these results and in the case of LTI or polytopic uncertain systems, the user can also call for less conservative results involving slack variables. These conditions are not purely LMI but are associated with heuristics that have usualy good chance of success (guaranteed to be better than Lyapunov Schaping Paradigm inthe discrete-time case). Publications related to these results are [PeaPhd], [Arz00] and [Far05].
Randomized analysis of uncertain systems
The current version of R-RoMulOC includes randomized analysis of uncertain systems subject to various uncertainty structures. In particular, Monte Carlo randomized algorithms, which provide a probabilistic approximation of the performance function that needs to be evaluated, are constructed. This approximation is based upon the multisample, which is generated according to the given density function describing the uncertainty. Given probabilistic parameters, called accuracy and confidence, the sample complexity (which is the minimum cardinality of the multisample) is computed using the (additive) Chernoff bound. Similarly, the log-over-log bound is used for computing the worst-case performance. Publications related to these results are [TeCaDa:13], [CaDaTe:00], [CalDab:02], [TeBaDa:97].
Randomized design methods for probabilistic LMI problems
The algorithms implemented in R-RoMulOC follow a general iterative scheme, which consists of successive randomization steps to handle uncertainty and optimization steps to update the design parameters. These algorithms share two fundamental ingredients: probabilistic oracle and update rule. For the probabilistic oracle, a random check is performed with the objective to assess whether the probability of violation of the current solution is smaller than a given level. In this case, a certificate of unfeasibility is returned. For the update rule, convexity of the problem is exploited, for constructing a new candidate solution. Publications related to these results are [TeCaDa:13], [CaDaTe:11], [DabTem:10],



projects.laas.fr/OLOCEP/rromuloc - last update 9-Jan-2014